To address a previous confusion, complementary angles are angles which add up to 90º and supplementary angles are angles which add up to 980º. A good way to not confuse them ever again is noticing that the “c” has only one angle inside while the “s” has two. Also, c stands for corner while s stands for straight!
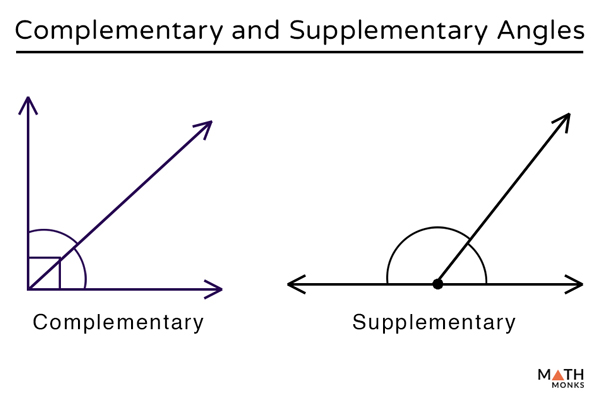
Everything to Know about Angles
Angles in Intersecting Lines
There are a few basic angles in intersecting lines. First of all, opposite angles are always equal. Opposing angles are just as its name suggests. Second, if a straight line is cut by another intersecting line, then any two adjacent angles will be supplementary to each other, or two angles on a straight line always add up to 180º. Those theorems will come in very useful when trying to prove other theorems!
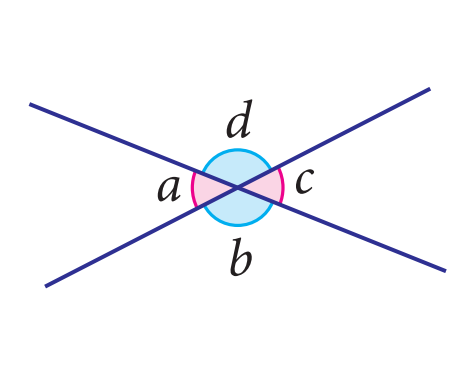
- First Theorem: a = c, b = d
- Second Theorem: a + b = a + d = b + c = d + c = 180º
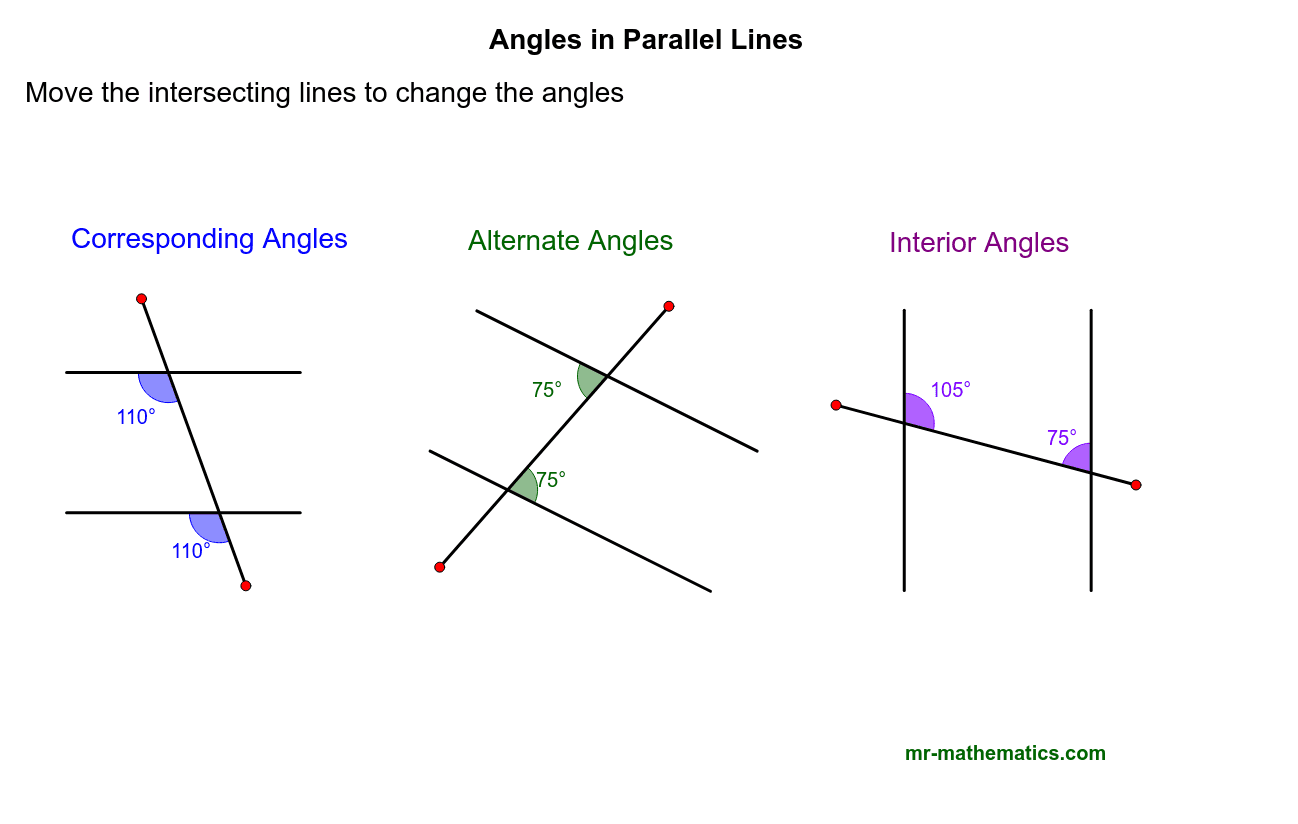
Angles in Parallel Lines
There are three main types of angles in parallel lines. All of them appear when two (or more) parallel lines are cut by a transversal, which is a line not parallel but intersecting the two parallel lines. The first type is corresponding angles, where the angles are in the same position. Corresponding angles are always equal. A good way to remember this is to think of the word “correspond”, meaning “match or agree almost exactly”. The second type is alternate interior and exterior angles. This is where the position of one angle is opposite of another. Alternate angles are always equal. You could also easily remember this type of angle with its name. Finally, there are interior angles, where they are on the same side of the transversal. Interior angles are supplementary. You could remember the shape by the word “interior”. If you forgot the three rules, draw a parallel line and transversal yourself!
Everything to Know about Triangles
Special Points
- This section is slightly advanced and not required to completely memorize
There are a lot - and I mean A LOT - of special points in triangles. However, four of them are really important. Before we get to them, we should put a few definitions. An altitude of a triangle is called 高 in Chinese, but as this is going to be mainly English, this is just FYI. An angle bisector is a line which splits an angle equally in half, or in this context, the line from a side which splits the side’s opposite angle in half. The median, in this context, is the line drawn from a vertex to the midpoint of that vertex’s opposite edge. And finally, perpendicular bisectors are lines perpendicular to an edge, drawn from the midpoint of that edge. The first point is called the orthocenter, which is the intersection of the three altitudes. The orthocenter is used to distinguish triangles by their largest angle: It would be inside an acute triangle, on the vertex of a right triangle and outside obtuse triangles. The second point is called the incenter, which is the intersection of the three angle bisectors. This point is the center of the largest possible circle which can be inscribed in a triangle. The third point is centroid, or the intersection of the three medians. This is the center of gravity for the triangle, and so it is more commonly used in physics than in maths. Finally, there is the circumcenter, the intersection point of the three perpendicular bisectors. This is the center of the smallest circle which would have the triangle perfectly inscribed within it.
ADDITIONAL READING: https://www.matematica.pt/en/cheatsheet/triangle-points.php
Angle & Congruence Theorems
There are also multiple angle theorems in triangles. First of all, all interior angles add up to 180º. Don’t laugh - competitions would find trickery and black magic to make this single theorem a lot more complicated, and you could get a wrong answer on this! Second, the base angles of an isosceles triangle are congruent. In graphical explanations or proofs, this would come in very useful. The third theorem - and I heard that this is being learnt in math class - is that an exterior angle is equal to the sum of the two other interior angles. This is because both the exterior and interior and the three interior angles add up to 180º. They are explained very clearly in https://byjus.com/maths/triangle-theorems/#:~:text=Theorem%201%3A%20The%20sum%20of,a%20triangle%20is%20180%20degrees.&text=Theorem%202%3A%20The%20base%20angles%20of%20an%20isosceles%20triangle%20are%20congruent.&text=The%20angles%20opposite%20to%20equal,are%20also%20equal%20in%20measure.
Finally, there are the laws of congruence. There are five rules of congruence: SSS (Side-Side-Side, not student support service), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side) and RHS (Right Angle-Hypotenuse-Side). I won’t experience then too much, but visit https://www.cuemath.com/geometry/congruence-in-triangles/ for more. Don’t worry if you cannot remember them all; just remember that AAA (Angle-Angle-Angle) is the only similarity theorem.